Series in Factor

Played around with Factor again. Still feels strange but is even more fascinating. I tried to implement some helper functions for series. The lesson I learned and what I like the most about Factor: code is data!!! I think Factor surpasses by far the possibilities of Lisp with its defmacro system. Slowly I realize the meaning of a concatenative language.

Here is the code:


! TODO:
! Define unit tests
! help files
! signatures
! parsing words

IN: series

USING: math words sequences kernel tools quotations arrays ;

TUPLE: il list quote ; ! il = infinite list

: get-il-list ( il -- seq )
dup il-list ;

: get-il-quote ( il -- quot )
dup il-quote ;

: unfold ( seq -- stackseq )
[ ] each ;

: push-next-element ( il -- )
over il-list push ;

: rev-il-list ( il -- )
get-il-list nreverse ;

: (pop-first-element) ( il -- element )
get-il-list pop ;

: pop-first-element ( il -- element )
rev-il-list (pop-first-element) ;

: remove-first-element ( il -- element )
pop-first-element >r rev-il-list drop r> ;

: calc-next-element ( seq -- element )
get-il-quote >r get-il-list unfold r> call ;

: il-next ( il -- next )
calc-next-element push-next-element remove-first-element ;

: repeat-if ( il-quot crit-quot -- el ) ! acts as a filter
over call 2dup swap call [ 2nip ] [ drop repeat-if ] if ;

: collect ( n quot -- seq )
V{ } -rot [ add ] append times ;

: not-dividable ( n divisor -- ? )
mod zero? not ;

: naturals ( -- n )
V{ 1 } [ 1+ ] <il> il-next ;

: squares ( -- n )
V{ } [ naturals dup * ] <il> il-next ;

: ones ( -- n )
V{ } [ 1 ] <il> il-next ;

: from2 ( -- n )
V{ 2 } [ 1+ ] <il> il-next ;

: factorial ( -- n )
V{ 1 } [ from2 * ] <il> il-next ;

: powers-of-two ( -- n )
V{ 1 } [ dup + ] <il> il-next ;

: fib ( -- n )
V{ 0 1 } [ + ] <il> il-next ;

: odds ( -- n )
[ naturals ] [ odd? ] repeat-if ;

: evens ( -- n )
[ naturals ] [ even? ] repeat-if ;

: (primes) ( -- )
V{ 2 } [ 1+ ] <il> il-next ; ! => from2

: call-word-def ( word -- res )
word-def dup call dup ;

: prime-criteria ( n -- quot )
[ not-dividable ] curry ;

: gen-quot ( -- quot )
\ repeat-if 3array >quotation ;

: update-word ( x y z -- word-def )
rot define-compound ;

: primestep ( word -- n )
dup >r call-word-def >r prime-criteria
gen-quot r> r> update-word ;

: primes ( -- n )
\ (primes) primestep ;

PROVIDE: demos/series ;



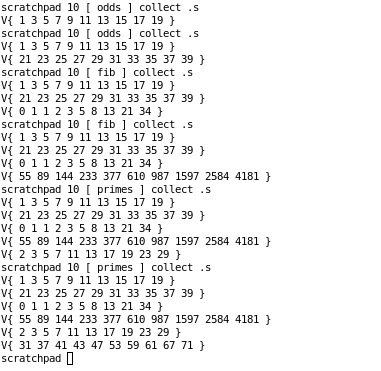
You can use it as follows, e.g.

1. naturals returns because its invoked the first time "1"
   
2. naturals returns "2"
   
3. 10 [ primes ] collect returns the first 10 primes in a vector
   
4. 10 [ fib ] collect returns the first 10 fibonacci numbers in a vector
   

Here is a screenshot: